Science and miracles

So on the one hand we have science and on the other we have miracles, right? Miracles are kind of what science debunks. People who believe in miracles lack scientific understanding. Because miracles simply don’t happen. They just can’t. Because nature follows laws. And those laws are what science discovers.
Well, let’s try another perspective. What if science makes miracles possible? And then you would maybe say that I’m using miracles in another sense than what I did in the paragraph above. Because these miracles would not go against the laws of nature but rather use the laws of nature. And I would say you are right. With a caveat. Science itself debunks older science and in that sense, science changes the laws of nature. In some sense. But of course, new science doesn’t change the laws of nature, new science just discovered what was always true. It just expands our knowledge of the laws of nature. And in doing that it makes things possible that in our earlier understanding of nature seemed impossible. Science transforms our understanding of the laws of nature and then at the same time changes the space of possibilities. And this is a movement with seemingly no end. The history of science is a history of advancements and there is no reason to think that this movement would have a limit.
Albert A. Michelson, a physicist who performed experiments in the late 19th century showing that the speed of light was the same for all observers, said in a lecture in 1894 that "... it seems probable that most of the grand underlying principles have been firmly established ... An eminent physicist remarked that the future truths of physical science are to be looked for in the sixth place of decimals.”. The physicist Max Planck has reported that a similar sentiment was expressed by Philipp von Jolly, his professor of physics in the late 19th century. Both Philipp von Jolly and Albert A. Michelson of course turned out to be incorrect in their predictions. The 20th century came with possibly the most dramatic advancements and revolutions in our understanding of nature that has ever occurred in the history of science.
Today, the general consensus among scientists is, I think, rather that while we understand more than we ever have, there is still so much we don’t know. There are fundamental questions we don’t know the answers to in basically every part of science: in physics, in biology, in mathematics and so on.
So what science does is to make new discoveries and deepen our understanding of nature. And this seems to be an adventure with no end. But then what do the laws of nature mean if they constantly change as science advances?
Particularly in physics there still is this idea of the final theory. Many physicists still seem to believe in the idea of a final theory that would explain everything in some simple and beautiful mathematical equations. This would be a theory that basically stops science in its movement. At the same time this is an idea that has been criticized by other physicists, and rightly so I think. And I would guess that today the majority of physicists actually don’t believe in the existence of a final theory, and I would also think that the ones who believe in it are fewer and fewer. In that sense the physicists are coming to terms with physics in particular and science in general as a sort of infinite game.
The most simple argument against this idea of a final theory of everything is to point out that this theory would have to be an explanation of itself. This seems to give something like a circular argument. Theories generally are not explanations of themselves but of some limited phenomena. A theory that also explained itself would in some sense resemble the problem in logic that arises when trying to analyze the sentence: This sentence is true. If a sentence says of itself that it’s true, is it then true? Well, regardless of the answer you give to that, the sentence itself is not very meaningful. It doesn’t really seem to say anything. And that is maybe the only theory of everything we could have. That it is true. Something along these lines was formulated already by the greek philosopher Parmenides. In his poem On nature a goddess simply says that the truth is that everything is. She also says that what is not is not. This seems like two obvious truths, and still, we can debate, and it has been debated ever since, if Parmenides didn’t already say too much.
So that should make us a bit cautious about the possibility of a final theory.
What is also stated explicitly by the goddess in Parmenides poem, but often forgotten in the discussion of it, is that this truth of being is not accessible to anyone mortal. We should assume that Parmenides' opinion was that the oneness of everything can not be experienced by a human being. At least it’s not accessible to reason and can therefore only be expressed in a poem.
I think one reason the argument that a final theory of everything would have to explain also itself is not immediately convincing to everyone, and also to be honest not to me either, is that it isn’t obvious that the theory itself is part of the reality it is describing. And if the theory isn’t part of the reality it describes then it wouldn’t have to describe itself. A theory doesn’t seem to be, at least not only, a physical entity and what the physicist wants to describe with the final theory of everything is the totality of matter, because that’s exactly what physics is supposed to describe. This description will be written in mathematics and now I’m guessing but I think that the prevalence of Platonists among mathematicians is quite high. That is, many mathematicians think of themself as working in another dimension than the physical one. They are working with ideal objects, not material objects. Kurt Gödel is one example of this, and a very recent one in the history of mathematics. That Kurt Gödel was a Platonist can be surprising because his results about incompleteness in mathematics seems to show that, specifically, we will never have a final theory of all of mathematics. One of his results in mathematical logic shows that mathematics as we know it contains true propositions that are unprovable. He also showed that mathematics cannot prove it’s own consistency, which means that it cannot prove that it will not contain contradictions. So for Gödel we can see that there was no contradiction between the fact that we will never have a complete theory of mathematics and the idea that mathematics is a science of ideal objects, unaffected by time and space.
And really, how could it be any other way? If mathematics describes the reality of space and time, then the mathematical formulas themselves can’t also be changing. The laws of change of physics must be unchanging, fixed in some sense, to be able to do its job of describing the very change it is describing, right?
And at the same time, we know that these formulas describing space and time have at least one time been replaced by new ones. We live in the post-einsteinian world. And that world is in many ways profoundly different to the pre-einsteinian world, which for a couple of hundred years was the post-newtonian world, which in turn was different to the pre-newtonian world… The post-einsteinian world is of course recognized for example by the presence of nuclear power plants and nuclear bombs. These two phenomena in themselves, it could be argued, changes our relationship to time. Maybe most obviously the nuclear bomb, that has in some sense on its own ushered humanity into a new kind of apocalyptic time. The nuclear bomb was made possible by the insight into the relation between energy and mass derived by Albert Einstein in 1905 from his theory of special relativity, and later famously expressed as E = mc2. But the theory of special relativity is also a theory of time itself. It says that the length of a certain time interval is experienced differently depending on the relative position and velocity of different observers. So if Isaac Newton assumed a concept of absolute time, Einstein showed that this assumption is only valid as an approximation when observers move very slowly compared to the speed of light.
What are the consequences of this relativity of time itself? I think it’s safe to say that they are far-reaching and profound. And also of course counter-intuitive, which is easily explained by the fact that we generally move around in relative velocities far from the speed of light, and thus the idea of an absolute time still seems very reasonable to most of us. And maybe even to physicists.
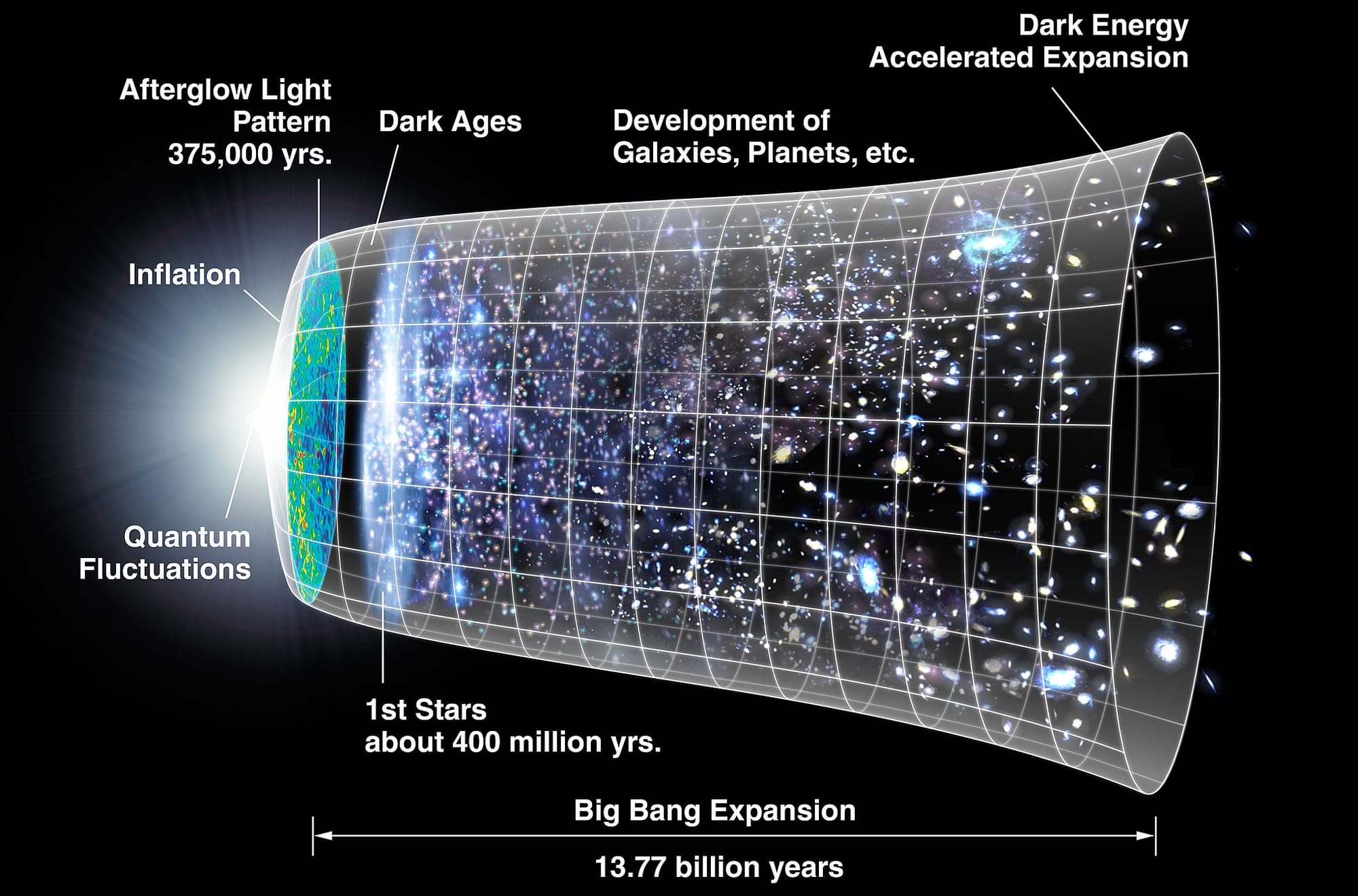
Because, I wonder, how can we measure the age of the universe if there is no absolute time? In the pictures sometimes presented of our universe with a beginning in a point that expands into a sort of tube and then with an open end around 13,8 billion years later we "see” the entire history of the universe from the outside in a god-like perspective. Of course this is just a sort of graphic that is not to be taken too seriously, but still, in this graphic there seems to be an implicit concept of absolute time that rules our universe. It’s as if we have taken our relativistic einsteinian universe and placed it back into the newtonian universe with absolute space and time. And again, it’s only a picture, but I wonder in what framework except for exactly the newtonian framework implied in this picture that the age of the universe becomes a meaningful concept?
At this point I should stress that I am a non-expert with very limited knowledge of physics. My perspective on physics is as someone more trained in analyzing concepts than reading mathematical formulas. And of course you need to be very fluent in the mathematics of physics to get a full understanding of it. So, again, my understanding is limited. However, it’s also the case that physics is not only the mathematical formulas, there’s also fundamental concepts guiding the physicist in his or her finding and later interpretation of these formulas. Einstein is probably on of the most obvious example of this.
An indication of the level to which Einstein's relativistic universe goes beyond our basic intuitions, and how maybe even the physicists intuitions is still lagging behind here is the paper published a couple of months ago that suggests that what is called dark energy, and which have been an established concept in physics for at least a couple of decades now, might actually not exist. The phenomena that dark energy is supposed to explain, namely the seeming accelerating expansion of our universe, might instead simply be explained, this paper suggests, by how heavy objects (in this case galaxies and clusters of galaxies) slows down time. This is called gravitational time dilation and is yet another consequence of the theory of special relativity. This for me points to the possibility that even after learning Einstein's theories and also becoming skilled in doing the calculations connected to them, the fundamental shift in our concept of time that they imply might not be fully appreciated; and that the newtonian framework with an absolute space and time hasn’t completely lost its grip on the minds of our cosmologists. Put in other words: the einsteinian revolution is still underway.
I think this revolution has some philosophical consequences. For example, the idea of eternity becomes less intelligible. If there is no absolute time, then what does eternity mean? If time is relative, then what does eternity relate to? And if there is no eternity, then what happens to Plato's theory of forms? What happens to the ideal objects of mathematics?
And this brings us back to Gödel the Platonist, and the question: is it possible to be a Platonist after the theory of relativity?
I think it isn’t really. The theory of relativity is part of a storm sweeping through the last 200 years or so that are bringing down at least a naive form of Platonism. Plato lived through a dramatic evolution in the science of mathematics, with the development of the concept of an axiomatic system. The Elements of Euclid, written around 300 BC, was the crowning achievement of this. But the general theory of relativity, presented in an article in 1915, wouldn’t have been possible without developments in mathematics in the 19th century that partly undermined euclidean geometry. This is the story of the 5th postulate and non-euclidean mathematics. What was invented was a geometry where it is possible for parallel lines to intersect (elliptic geometry) or drift away from each other (hyperbolic geometry). It was possible to formulate a consistent geometry where the 5th postulate of euclidean geometry was discarded. What Einstein later showed with the general theory of relativity was that we actually live in the world of non-euclidean geometry, not the world of euclidean geometry.
As I wrote above I think we are still living in the reverberation of that revolution. Because what was also brought down was the rigid distinction between space and time that seems to underlie Plato's theory of forms, where true ideas are eternal and space is temporary and understood as the domain of illusion. Instead it turns out that classical euclidean geometry, the paradigm of truth for almost 2000 years, is in a sense an illusion.
Part of the inspiration for this text came from a book I had never heard of until about a month ago. The book is A Course in Miracles and came out in 1976. It was mentioned in a video on a Youtube channel that was recommended to me by the algorithm. Apparently it is a relatively influential book through later interpreters of the book as Marianne Williamson and also Eckhardt Tolle. The book itself was written by Helen Schucman. She was a professor in medical psychology at Columbia University in New York. Allegedly, in 1965, she started hearing a voice speaking to her that identified itself as Jesus and that also asked her to take notes of what it said. She wrote the book between 1965 and 1972. It was later published in 1976, spanning over 1,300 pages.
I started reading it and found it interesting. It can be read as an interpretation of Christianity that seems to have borrowed ideas from Indian religious texts, particularly the Upanishads.
I later found an article about A Course in Miracles written by Sheila Heti in the 2024 september issue of Harper’s magazine. It’s an interesting article written from a very personal perspective. But she also makes some pretty thorough research into how the book came to be. And one thing that seems very possible, or at least difficult to rule out, is that CIA were somehow involved via William Thetford, Helen Schucman’s friend and colleague at Columbia University.
What I took from the book is the idea of miracles as something almost ordinary or normal, and the consequences that this has for our understanding of time. In this text I tried to connect that to science, and a certain movement of science that is always in some sense going beyond itself. What is possible in a culture in a given time and place is decided by the models of the world available to this culture in that very time and place, and if those models are improved new possibilities can emerge. This can make the impossible possible, and can in that sense be called a miracle. I also think the concept of miracle can to some extent be applied to the very improvement of the model, the advancement of science itself. We have different ideas of what we call the scientific method, but in the end we have no rules for how to advance in our understanding of the world. There is always necessarily an element of something beyond reason when we improve on our understanding of the world, because reason is exactly defined by the very model we are improving on.
In an upcoming post I will continue this discussion and also more generally look into the relation between science and religion in the ”west” and the ”east” respectively.